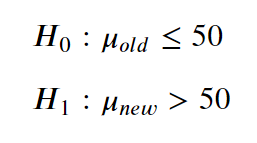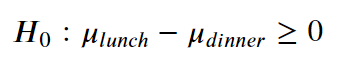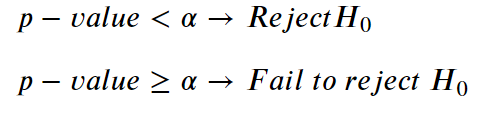Must-read Guide to Hypothesis Tests You Will Never Use
여러분이 사용하지 않도록 설명된 통계의 가장 큰 개념
Photo by Jean-Daniel Francoeur from Pexels
Demotivation
시작부터 여러분의 희망을 내려보자. 여러분이 데이터 과학자인 직업을 갖을 때까지 이 글의 개념은 사용하지 않을 것이다. 여르문은 공공 데이터셋에서 이를 몇번 연습할 것이고 그것이 다일 것이다.
그러면 왜 이런 개념을 공부할까? 여러분이 실제 직업을 구하면 에베레스트에서 던져진 아기새같지 않기를 바라기 때문이다. 그럼 이 글에서는 무엇에 대해 다룰 것인가?
우리는 비즈니스와 과학적 연구에서 데이터 관련 프로젝트를 끝내는 케이크 장식 - 가설 검정(hypothesis testing)에 대해 다룬다. 가설 검정은 결과가 우연인지 아니면 실제 의미있고 중요한 지를 테스트한다.
예를 들면, 의료팀은 두 테스트 그룹에 신약을 제공고 회복 시간, 부작용 등과 같은 지표를 비교하여 유효성을 측정한다. 결과가 "있는 그대로(as is)" 받아들여지지 않는 이유가 있다.
통계적 용어로 이는 샘플 통계(sample statistics)를 확인하여 모집단 파라미터(population parameter)에 대한 예측을 하는 것과 같다. 즉, 결과를 확실하게 하는 것은 샘플에 국한되지 않고 일반적인 모집단에 적용한다.
가설 검정은 조건부 확률(conditional probability), 분포(distributions), 신뢰구간(confidence intervals) 등과 같은 통계와 확률의 많은 개념을 사용한다. 세련된 용어로 여러분을 겁주려 하지 않지만 가설 검정을 둘러보는데 시간이 걸린다. 따라서 여기서는 코드로 작성해 보기 전에 개념을 전체적으로 알기 위해 주로 이론에 집중한다.
Real-World Example
솔직히 조각을 모으는데 오랜 시간이 걸렸지만 모든 것을 클릭하게 만든 리소스는 Khan Academy의 hypothesis testing playlist였다. 여러분에게 첫번째 아이디어를 제공하기 위해 칸 이카데미의 예제중 하나를 사용한다.
4형제 Jon, Bruce, Harry, Bob이 있다. 매일 누가 설걷할지 정하기 위해 Jon이 가방에서 무작위로 이름을 뽑기로 한다.
잇달아 4일 동안 Jon가 선택되지 않아 Bruce가 의심하기 시작한다. Bruce는 Jon이 속이고 있지만 확지하지 않다는 가설을 세우고 몇일 더 기다리기로 한다. 10일째에 Jon은 여전히 뽑히지 않았다. 이번에 Bruce는 Jon이 확실하게 속이고 있고 그의 확률 기법으로 이를 테스트해야 한다고 생각한다.
안전하게 Bruce는 Jon이 결백하다는 추측으로 시작하지만 확률이 20%보다 작게 되면 Bruce는 안전하게 부모님게 Jon이 속임수를 쓰고 있다고 말할 수 있다.
모두가 25%로 뽑히는 동일한 확률이 주어지면 뽑히지 않을 확률은 75%이다.
Bruce는 조합확률(joint probability)로 10일동안 뽑히지 않는 확률을 계산한다.
결과는 ~6%이거나 이 특별한 이벤트는 1000일마다 6번 발생한다. 결과는 Bruce의 의심수준보다 더 낮다. 따라서 Jon이 속이고 있다고 부모님께 말할 수 있다.
실생활에서 모든 가설 검정은 보통 이러한 패턴을 따른다. 우선 2가지 경쟁하는 아이디어가 만들어진다.(즉, 1. Jon이 결백하다와 2. Jon이 속이고 있다.) 그리고 샘플데이터(즉, 10일도안 무작위로 선택한 관측된 결과)를 사용하여 테스트 통계가 우연히 발생한 것인지 아니면 새로운 측정치인지가 점검된다.
귀무가설 : 일반적으로 맞다고 가정하는 가설 (Jon이 결백하다)
대립가설 : 새롭게 맞다고 증명하는 가설 (Jon이 속이고 있다)
이 시점에서 의문이 발생한다. "어떻게 결과가 무작위인지 아니면 새로운 측정치인지 알 수 있는가?" 여기서 유의 수준(significance level)이 작동하기 시작한다. 위 예제에서 Bruce는 20%의 유의수준을 설정하고 그의 테스트가 유의수준보다 낮다면 Jon이 결백하다는 그의 가설을 기각(reject)하고 jon이 속이고 있다고 결론지었다.
비즈니스와 연구에서 이 유의수준은 보통 5%로 설정한다. 의료 분야에서는 1%이다.
가설검정은 모집단 파라미터에 대한 것이다.
가설검정에서 모집단(population)과 샘플(sample) 두 용어가 널리 사용된다. 따라서 이를 구분하는 것이 중요하다.
- 모집단(population) : 흥미가 잇는 전체 그룹을 나타낸다. 예를 들면, Towards Data Science의 모든 구독자, 숩에 있는 모든 나무, 국가내 모든 사람들이 모집단으로 간주된다.
- 샘플(sample) : 모집단의 부분집합(subset). 예를 들면, 이 글의 독자는 Towards Data Science 구독자의 작은 샘플이다. 또한 한 병원에서의 감기 환자는 지구에서 감기로 진단된 모든 환자의 샘플이다. 모집단으로부터 무한히 많은 샘플의 변형이 있을 수 있다.
- 모집단 파라미터(parameter) : 모집단에 대한 전역 통계(global statistics). 예를 들면, 지구상 모든 인류의 평균 키 또는 몸무게는 파라미터로 간주된다.
- 샘플 통계(statistic) : 하나의 샘플에 국한된 값
가설(hypotheses) 수립
가설검정의 첫번째 단계는 경쟁하는 가설(competing hypothesis)을 서술하는 것이다. 대립가설은 반대이고 겹치는 부분이 없어야만 한다. 예를 들면, "유죄(guilty)가 입증될 때까지 무죄(innocence)"인 가설로 각 케이스를 시작하는 사법 시스템을 예로 들 수 있다.
용어에서 대립 가설은 귀무가설(Null)과 대립가설(alternative)이라고 한다. 어떠한 데이터 또는 증거 없이 귀무가설을 믿는다. 이는 또한 "차이 또는 영향이 없음" 가설로써 생각 할 수도 있다. 법정에서 모두는 증거가 제시될 때까지 무죄로 간주된다.
이것이 Bruce가 Jon이 결백하다는 생각으로 시작한 이유이다. 이를 설정하는 방법 때문에 귀무가설을 수용하는 것은 비즈니스 또는 연구 두 분야에서 결정에 어떠한 영향도 미치지 않을 것이다.
이름이 제시하는 것처럼 대립가설(alternative hypothesis)은 귀무가설의 반대이며 또한 입증하거나 달성하길 바라는 아이디어이다. bruce는 Jon이 속이고 있다는 것을 입증하길 원한다. 따라서 대립가설은 'Jon이 속이고 있다'가 된다. 법정에서 대립가설은 '기소된 사람은 유죄이다'가 된다.
표기법으로 가면 귀무가설은 $H_0$로 나타내는 반면 대립가설은 $H_1$ 또는 때때로 $H_a$로 나타낸다. 수학을 사용하여 귀무가설은 보통 '등호(equal)' : $=, \le, \ge$의 종류와 함께 나타나지만 대립가설은 $<, >, \ne$ 같은 기호와 관련될 것이다.
위의 내용을 또다른 예제로 살펴보자. 웹사이트가 더 많은 트래픽을 유도하는지 점검하기 위해 새로운 UI를 테스트하고 있다. 소유주는 한달동안 총 트래픽의 평균을 비교하여 이를 점검하고자 한다.
이미 언급한 것처럼 어떠한 데이터를 보기 전에 귀무가설이 참이라고 믿는다. 이번 경우 한달동안 새로운 UI를 시도하는 것 없이
- 귀무가설은 "기존 디자인의 평균 트래픽은 새로운 디자인보다 좋거나 더 낫다"가 될 것이다.
그리고 새로운 UI에서 더 큰 트래픽을 입증 또는 달성하고자 한다. 따라서
- 대립가설은 "새로운 UI의 평균 트래픽은 기존 UI의 평균보다 더 크다"가 될 것이다.
표기법으로는 다음과 같을 것이다.
또다른 가설 조합 또한 가능하다. - 평균이 어떤값보다 더 크다.
여기서는 50보다 더 큰 평균 트랲픽을 달성하려고 한다. 따라서 트래픽이 이 값보다 같거나 더 작다는 가설로 시작한다.
또다른 조합은
마지막은 특정사례(case-specific)이다. 예를 들면, 일부 의학 테스트는 정부에서 수용하는 특정 정확도 접수가 필요하다. 위의 경우를 사용하여 관련된 가설을 만들 수 있다.
Types of Errors
가설검정을 포함하여 오류에 자유로운 실험 또는 조사는 없다. 보통 가설검정에는 1종(type 1)과 2종(type 2)의 2종류 오류가 있다.
- 1종 오류(Type 1 error) : 귀무가설이 참일 때 대립가설을 받아들이면 발생한다. 가장 나쁜 오류의 종류이다.
- 2종 오류(Type 2 eoror) : 대립가설이 참일 때 귀무가설을 받아들이면 발생한다. 1종 오류만큼 나쁘지 않다.
법정 예제로 계속하면,
배심원단이 어떠한 2종 오류가 발생하는 것을 피하기로 결심하면 결백한 누군가를 포함하여 모드를 유죄로 기소할 것이다. 이는 심각하게 많은 1종류가 있을 수 있다는 의미이다. 반대로 무슨수를 써서라도 1종 오류를 피하려고 한다면 범죄자를 포함하여 모드를 풀어줄 것이다. 이는 많은 2종 오류로 이어진다.
이러한 관계때문에 전문가들은 종종 가능한 많은 2종 오류를 피하려고 하는 동안 1종 오류의 수에 대한 임계치(threshold)를 설정한다. 따라서 이 임계치는 여러분이 사용하는 상황에 따라 달라진다. 비즈니스와 연구에서 이는 0.05로 설정한다. 즉, 100번마다 5개의 1종 오류를 수용하는 것에 반대하지 않는다. 의학 분야에서 임계치는 0.01이다.
그러나 1종 오류의 수가 수용할 수 없는 경우가 있다. 다음은 전체적인 시야로 모든것을 포함하는 예제이다.
여러분의 업무가 낙하산이 펴지는지 펴지지 않는지를 점검하는 것이라고 하자. 여러분은 모든 낙하산이 동작하기를 원한다 따라서 여러분은 각 아이템에 대해 다음 가정을 수립한다.
여기서 1종 오류의 임계치는 전적으로 수용 불가능하다. 왜냐하면 얼마나 희박하게 발생하는지 중요하지 않다. 어떠한 1종 오류라도 스카이다이버인 실제사람의 죽음을 의미하기 때문이다.
여러분이 명확하게 1종 오류와 2종 오류가 무엇인지 정의하는 것이 중요하다. 보통 다음과 같이 표를 그리는 것이 도움이 된다.
1종 오류에 대한 임계치는 그리스 문자 $\alpha$로 표시하고 false positive라고 한다. 비슷하게 2종 오류는 $\beta$로 표시하고 false negative라고 한다.
Hypothesis Testing Pipeline
지금까지 가설검정에 대한 처음 두 단계를 알아보았다.
- 귀무가설과 대립가설 수립
- 오류 종류 확인 및 유의 임계값(significance threshold) 설정
이제, 파이썬으로 간단한 예제를 살펴보자.
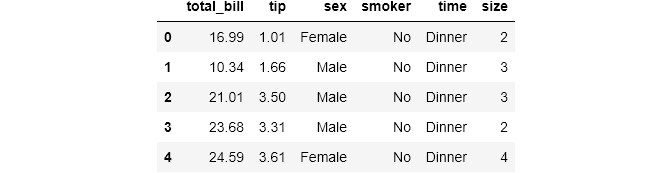
다음은 레스토랑에 방문한 244명의 고객을 포함하는 seaborn의 tips 데이터셋이다. 데이터셋은 청구금액과 팁 총액, 테이블 크기 및 다른 상세 정보를 기록한다. 간단하게 여러분이 레스토랑 소유주이고 데이터셋이 한주간 정보를 포함한다고 해보자.
tips = sns.load_dataset('tips').dropna().drop('day', axis=1)
>>> tips.head()
여러분은 결과를 dinner와 lunch 두 그룹으로 나누어 그날의 평균 수입을 계산한다.
>>> tips.groupby('time')['total_bill'].mean()
time
Lunch 17.168676
Dinner 20.797159
Name: total_bill, dtype: float64
평균에서처럼 저녁시간 고객이 더 많은 비용을 지불했다. 이제 여러분은 이것이 단지 그 날에만 국한된 무작위 이벤트인지 아니면 모든 추가적인 고객이 저녁에 더 많이 비용을 지불한다는 의미인지 궁금하다. 가설검정을 사용하여 이를 점검해 보자.
저녁시간 고객이 비용을 더 많이 지불한다는 것을 입증하고 싶기 때문에 이는 대립가설이 될 것이다.
- $\mu$는 레스토랑에서 다가오는 모든 날동안 다른 주간 평균 수입인 모집단 평균을 나타낸다.
이 가설검정의 형태를 수행하는 것은 점심시간과 저녁시간의 두가지 샘플을 가지고 있기 때문에 2개 샘플 테스트(two-sample test)라고 한다. 따라서 여러분은 종종 다음과 같이 표시된 두개의 샘플에 대한 귀무가설과 대립가성을 볼 것이다.
다음 단계는 $\alpha$ 임계치를 설정하는 것이다. 5%가 최고의 선택이다. 그리고 귀무가설에서 데이터를 시뮬레이션한다. 위 예제의 경우, 두개의 샘픔을 아주 많이 부트스트래핑하고 각 반복에서 평균으로 차이를 찾는다.
즉, 평균으로 차이의 샘플링 분포를 얻는다.
우선, 배열에 두 식사시간의 총 비용을 저장한다.
lunch = tips.query('time == "Lunch"')['total_bill']
dinner = tips.query('time == "Dinner"')['total_bill']
>>> tips.head()
참고로 다음은 평균간 차이이다.
>>> dinner.mean() - lunch.mean()
3.628
이제, 평균으로 많은 차이를 찾기 위해 두개의 샘플을 부트스트랩한다.
# Create an empty array to store the means
diffs = np.empty(10000)
for i in range(10000):
# Sample lunch
bs_lunch = np.random.choice(lunch, size=len(lunch))
# Sample dinner
bs_dinner = np.random.choice(dinner, size=len(dinner))
# Append the diff in means to diffs
diffs[i] = bs_dinner.mean() - bs_lunch.mean()
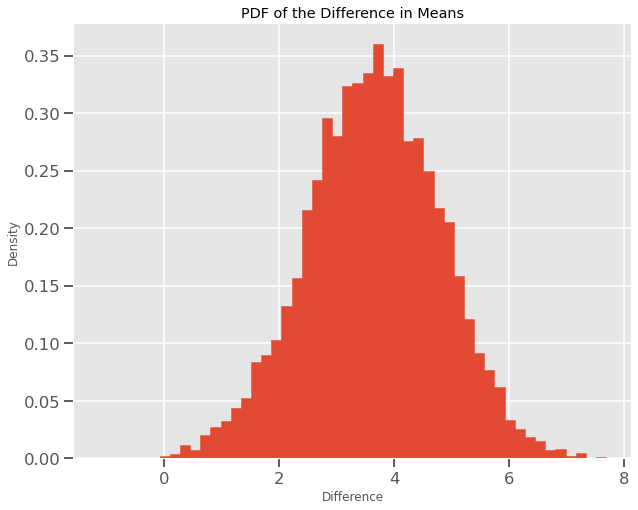
샘플링 분포를 도표로 그리는 것은 이것이 정규분포를 따른다는 것을 나타낼 것이다.
# Create fig, ax objects
fig, ax = plt.subplots(figsize=(10, 8))
ax.hist(diffs, histtype='step', fill=True, bins=50, density=True)
# Labelling
ax.set(title='PDF of the Difference in Means',
xlabel='Difference',
ylabel='Density')
plt.show();
이제, 귀무가설이 참인지 아닌지를 알기 위해 0보다 작거나 같은 값의 비율을 찾는다. 왜냐하면 우리의 귀무가설이 다음과 같기 때문이다.
이는 간단한 수학으로 계산될 수 있다.
np.sum(diffs <= 0) / len(diffs)
0.0003
0보다 작거나 같은 차이의 수를 찾고 샘플링 분포의 길이로 나눈다.
이는 평균으로 0보다 작거나 작은 차이를 갖는 0.0003인 확률을 제공한다. 이것의 의미는 무엇일까?
이는 우리가 귀무가설을 기각(reject)해야 한다는 것을 의미한다. 왜냐하면 점심시간동안 평균 수입이 저녁시간과 같거나 더 크다고 했기 때문이다. 그리고 우리는 이 추정으로 데이터를 시뮬레이션 하였고 추정이 발생하는 확률을 계산하면 0.03% 또는 10000일마다 3번인 것을 얻었다.
이를 기본으로 우리는 귀무가설을 기각하고 저녁시간 고객이 점심시간 고객보다 평균적으로 더 많은 비용을 지불한다고 서술한 대립가설을 수용한다.
이는 가설검증에 대한 간단한 예제였다. 참고로 다음은 전체 파이프라인이다.
- 테스트하고자하는 것을 찾는다.
- 관련된 귀무가설과 대립가설을 서술한다.
- 유의수준 $\alpha$를 설정한다.
- 테스트 통계(위 에제의 경우 평균을 사용하였다.)에 대해 귀무가설로 데이터를 시뮬레이션한다.
- 결과에서 결론을 내린다.
p-values, a true nightmare
주의깊은 독자는 위 예제에서 핵심 개념이 남아있는 것을 눈치챘을 것이다. 유의수준을 설정하였지만 이를 아무것도 참고하지 않았다. 그 이유는 유의 수준이 종종 p-값(p-values)과 함께 나타나기 때문이다.
다수를 위해 p-값(확률값, probability value)을 이해하는 것은 가설 검정의 가장 어려운 부분이다. 그러나, 여러분이 주의깊게 읽었다면 여러분은 거의 이미 이것을 알고 있다. 무엇을?, 어떻게?, 언제?
우리가 언제 0보다 같거나 작은 평균차이의 비융를 계산했는지 기억해 보자. 이 비율(proportion)이 p-값이다! 공식적인 맥락에서 우리는 종종 다음과 같이 p-값의 정의를 볼 수 있다.
귀무가설 유의 검정(null hypothesis significance testing)에서 p-값은 귀무가설이 올바르다는 추정으로 적어도 실제 관측된 결과만큼 극단적인 검정(test) 결과를 얻는 확률이다.
다음은 좀 더 간단한 정의이다.
귀무가설이 참인 세상에서 p-값은 귀무가설을 만족하는 조건을 관측하는 확률이다.
위 레스토랑 예제에 대한 정의로 변경하면
점심사간 고객이 저녁시간 고객과 동일하거나 더 많은 비용을 지불하는 세상에서 p-값은 0과 같거나 더 작은 두 식사시간 사이의 평균차이를 갖는 확률이다.
형제가 설걷이 대상을 뽑는 예제에서 p-값을 정의해 보자.
Jon이 결백한 세상에서 p-값은 10일동안 연이어 선택되지 않는 확률이다.
또다른 구체적인 예제를 보자. 여러분이 암을 탐지하는 새로운 테스트를 개발했다고 하자. 이 테스트를 정부가 수용하려면 99%이상의 정확도를 달성해야 한다. 따라서 이를 점검하기 위해 여러분은 귀무가설과 대립가설이 다음과 같은 가설검정을 사용한다.
여러분이 99%이상의 정확도를 갖기를 원하기 때문에 이는 대립가설이 된다. 이 경우, p-값은 귀무가설이 참이라고 추정하는 99%보다 더 낮은 정확도를 관측하는 확률이 될 것이다.
이제, 어떻게 p-값이 하나의 가설을 기각하거나 수용할까? 이곳이 유의수준(significance level)이 필요한 곳이다. 일반적인 경험법칙은 p-값이 $\alpha$보다 더 낮다면 귀무가설이 기각된다는 것이다. p-값이 $\alpha$와 같거나 더 크다면 아무것도 바뀌지 않는다.(항상 귀무가설을 수용하는것으로 시작한다.)
여러분은 또한 p-값이 $\alpha$보다 더 작다면 결과는 통계적으로 유의하다.(are statistically significant)고 통계학자가 말하는 것을 듣는다. 왜 그럴까?
우리가 항상 귀무가설이 참이라는 것을 수용하는 것으로 시작하는 것을 기억하자. 이는 귀무가설이 "새로운 것이 없음" 또는 영향없을을 나타내는 가설이기 때문이다. 우리는 어떤 데이터 또는 증거를 보지 않고 이를 수용했다. 그리고 결국에는 p-값이 $\alpha$보다 더 작으면 귀무가설을 기각하고 대립가설을 수용한다. 즉, 낮은 p-값은 우리가 무엇인가 '새로운' 그리고 대립가설에 속하는 무엇인가를 발견했다는 것을 제시한다. 이것이 p-값이 통계적 유의(statistical significance)와 관련이 있는 이유이다.
명확하게 p-값이 $\alpha$보다 더 높으면 우리는 귀무가설에 머물고 아무런 변화도 없고 유의(significant)한 것도 없다.
Statistical Significance(통계적 의미) vs Practical Significance(실제 의미), Dangers of Hypothesis Testing(가설검정의 위험)
가설검정은 비즈니스와 전문가에게 그들의 의사결정을 안내하기 위해 통계적 도구를 제공하는것에 대한 모든 것이다. 그러나 성공적인 그리고 통계적으로 유의(의미있는, significant) 결과가 항상 실제 유용한것은 아니다.
예를 들면, 웹사이트에 새로운 UI를 사용하려 한다고 해보자. 그래서 여러분은 원래와 새로운 디자인간 가설검정을 수행한다. 여러분은 CTR(Click-Thourgh Rate)가 기존보다 5% 더 높은것을 제시하는 통계적으로 의미있는 결과에 도달한다. 이것이 모든사람에게 새로운 UI를 즉시 배포한다는 의미일까? 반드시 그런것은 아니다. 왜냐하면 새로운 디자인이 기존보다 훨씬 더 비용이 들기 때문이다. 그리고 개선된 CTR은 미미하다. 실제로 여러분이 아무것도 바꾸지 않는게 더 나을 수 있을 것이다.
가설검정을 수행할 떼 너무나 많은 유사한 경우가 있다. 실제 수행대신에 언제든 여러분은 통계적으로 유의미한 결과를 보고 여러분의 결정에 대한 실제적인면을 고려한다.
게다가 가능한 데이터의 총량때문에 샘플크기는 점점더 커진다. 이는 샘플크기에서 작은 증가조차 통계적으로 의미있게 될 수 있지만 실용적이지 않은 결과일 수 있기 때문이다.
이것이 더 많은 비즈니스가 머신러닝을 도입하는 이유이다. ML 알고리즘은 각 고유한 데이터 포인트에 대해 가능한 결과를 예측하려고 한다. 반대로 가설검정은 일반적인 관점에서 전체 모집단을 비교한다.
예를 들면, 머신러닝 모델이 각 개인이 선호하는 아이스크림을 예측하지만 가설검정은 한가지 아이스크림을 선호도가 다른 선호도를 뛰어넘는지를 다룬다. 비즈니스 의사결정을 가설검정을 기초로 하면 여러분이 테스트하지 않은 다른 선호도는 말할 것도 없고 초코렛을 선호하는 전체 모집단을 무시할 것이다.
Conclusion
이 글에서는 단지 중요한 부분만을 다루어 여전히 배울 부분이 많이 남아있다. 특히 코드로 가설검정을 수행하는 것은 이론적인 이해와 코딩 능력 모두가 필요하다. 다음은 도움이 될 만한 다른 링크이다.