A 3-Minute Review of PCA: Compression and Recovery
A 3-Minute Review of PCA: Compression and Recovery
PCA의 유용한 시각적 표시
Photo by Jonny Clow on Unsplash
PCA does projection to reduce dimensionality.
직관적으로 PCA는 단지 데이터 포인트를 더 낮은 차원 초평면(hyperplane)에 직교선을 그리고 안착점(landing spot)을 찾는다. 초평면의 축은 포착하는 최대 분산(maximization of variance they capture)에 따라 선택된다. 포착된 분산이 클수록 투영(projection)이 포함하는 정보(information)가 더 많다. 이 축(axis) 선택 계획을 통해 PCA는 최소한의 정보손실을 달성하고 그 데이터를 훌륭하게 압축(compression)한다.
Wikipedia
Minimal example: the projection from 4D to 2D
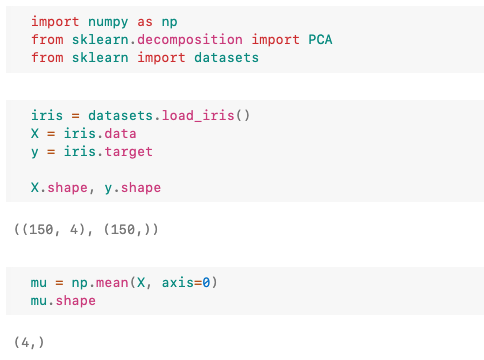
sklearn과 iris 데이터셋으로 어떻게 동작하는지 알아보자.
코드에서 150개의 예제와 4가지 특성 컬럼이 있는 것을 알 수 있다. 직접적으로 4차원 데이터를 시각화하기는 힘들다. sklearn.decompositon.PCA를 사용하여 2차원으로 투영해보자.
pc2는 주요 컴포넌트(principal components) 상위 2개의 순위이다. - 여기에 2열(row) 벡터가 있다. 이것들은 원래 특성 공간(original feature space)에 있기 때문에 4차원이다.
우리가 투영하는 2차원 평면은 pc2에서 이들 2개의 벡터(주요 컴포넌트)로 걸쳐진다. 이것이 평면의 기본 벡터(basis vector)로 이를 u, v라고 하자. 이 2차원 평면은 4차원 공간에 있다. 원래 특성 공간으로부터 - 4차원 공간의 관점, 원래 4차원 데이터 포인트를 이 2차원 평면에 투영하는 것이 PCA가 하는 것이다.
행렬 x_reduce는 (150, 2) 모양이다. 즉, 줄어든 2차원 공간에 150개의 예제가 있다. 각 열(row)은 2개 좌표를 가진 벡터이다. 첫번째 숫자가 u의 계수에 일치하고 두번째는 v의 계수에 일치하는 것을 기억하자.
이 방법으로 원래 (150, 4)인 데이터가 (150, 2)로 줄어든다/압축된다.
2차원으로 결과를 시각화하면 다음과 같다.
The Recovery from 2D to 4D
단지 시각화에만 관심이 있다면 관련 작업은 끝났다. 하지만 압축 계획으로써 PCA에 대해 훌륭한 것은 주요 컴포넌트(principal components), 투영(projections), 원본 특성 평균(mean)을 사용하여 원본 데이터에 아주 근접한 데이터를 복구할 수 있다.
x_recude는 2차원에 모든 투영을 포함한다. 간단하게 pc2로 행렬곱하고 평균을 다시 더하여 데이터를 복구시킬 수 있다.
행렬모양 : $(150, 2) \dot (2, 4) -> (150, 4)$
x_reduce에서 하나의 열(row), 즉 한번에 하나의 예제를 보고 좀더 명확하게 벡터 변환을 알 수 있다. Cu는 기본 u에서 좌표이고 Cv는 v에서 좌표이다.
이것이 2차원 투영에 4차원 주요 컴포넌트를 곱하여 2차원에서 4차원 데이터를 복구하는 방법이다. 마지막으로 평균을 다시 더하는 것을 잊지말자.
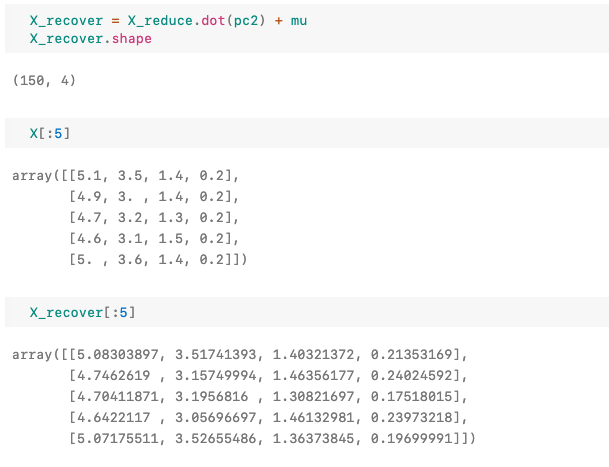
이제, 복구된 데이터가 원본에 얼마나 잘 근접하는지 보자.
얼핏봐도 복구가 꽤 잘 되었다고 말할 수 있다. 이것이 이미지는 여기 행렬과 많이 다르지 않기 때문에 PCA가 이미지까지 압축할 수 있는 이유이다.
끝이다. 이 작은 예제로 여러분이 고차원에서 PCA뒤의 선형대수에 대한 감각을 얻고 언제 이것을 사용할지 알 수 있기를 희망한다. 내부적으로 주요 컴포넌트를 찾는 절차에 관심이 있다면 온라인에 그에 관련된 자료가 많이 있다. 검색 키워드는 'SVD(Singular Value Decompositon)'이다.
좀더 일반적인 요점은 이것을 사용하기 위해 어떻게 알고리즘을 구현하는지 알 필요가 없다는 것이다. 많은 알고리즘들이 그 내용을 추상화하였기 때문이다. 반면에 어떻게 구현하는지 알더라도 여전히 실제 문제를 마주하면 언제 어떻게 적절하게 이를 사요하는지 오판할 수 있다. 적절한 응용에 대한 직관을 추출하는 것이 핵심이다.
다음은 관심이 있을 수 있는 다른 글의 목록이다.